Reverse regression continued. Suppose that the model in Exercise 5 is extended to y = x?? + d + , x = x?? + u.

Reverse regression continued. Suppose that the model in Exercise 5 is extended to y = βx?? + γd + ε, x = x?? + u. For convenience, we drop the constant term. Assume that x??, ε and u are independent normally distributed with zero means. Suppose that d is a random variable that takes the values one and zero with probabilities π and 1 ?? π in the population and is independent of all other variables in the model. To put this formulation in context, the preceding model (and variants of it) has appeared in the literature on discrimination.We view y as a ??wage?? variable, x?? as ??qualifications,?? and x as some imperfect measure such as education. The dummy variable d is membership (d = 1) or nonmembership (d = 0) in some protected class. The hypothesis of discrimination turns onγ a. What is the probability limit of c, the least squares estimator of γ, in the least squares regression of y on x and d? Now suppose that x?? and d are not independent. In particular, suppose that E[x?? | d = 1] = μ1 and E[x?? | d = 0] = μ0. Repeat the derivation with this assumption.

b. Consider, instead, a regression of x on y and d. What is the probability limit of the coefficient on d in this regression? Assume that x?? and d are independent.

c. Suppose that x?? and d are not independent, but γ is, in fact, less than zero. Assuming that both preceding equations still hold, what is estimated by (y | d=1) ?? (y | d = 0)? What does this quantity estimate if γ does equal zero?

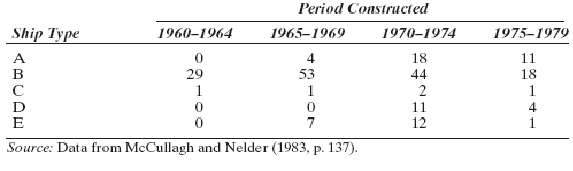
Ship Type ABCDE 1960-1964 10 29 1 Period Constructed 1965-1969 4 53 1 10 0 0 7 Source: Data from McCullagh and Nelder (1983, p. 137). 1970-1974 84212 44 11 1975-1979 11 18 1 4 1