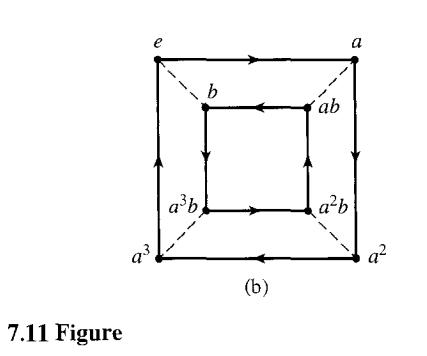
A relation on a set S of generators of a group G is an equation that equates some product of generators and their inverses to the identity e of G. For example, if S = {a, b} and G is commutative so that ab= ba, then one relation is aba^-1 b^-1 = e. If, moreover, b is its own inverse, then another relation is b² = e. 

a. Explain how we can find some relations on S from a Cayley digraph of G. 

b. Find three relations on the set S = {a, b} of generators for the group described by Fig. 7.11 (b).

 

Transcribed Image Text:

7.11 Figure e q³ b a³b, (b) ab a²b a a²