Consider a cube that exactly fills a certain cubical box. As in Examples 8.7 and 8.10, the
Question:
Consider a cube that exactly fills a certain cubical box. As in Examples 8.7 and 8.10, the ways in which the cube can be placed into the box correspond to a certain group of permutations of the vertices of the cube. This group is the group of rigid motions ( or rotations) of the cube. (It should not be confused with the group of symmetries of the figure, which will be discussed in the exercises of Section 12.) How many elements does this group have? Argue geometrically that this group has at least three different subgroups of order 4 and at least four different subgroups of order 3.
Data from in Example 8.7
An interesting example for us is the group S3 of 3! = 6 elements. Let the set A be { 1, 2, 3}. We list the permutations of A and assign to each a subscripted Greek letter for a name.
The reasons for the choice of names will be clear later. Let
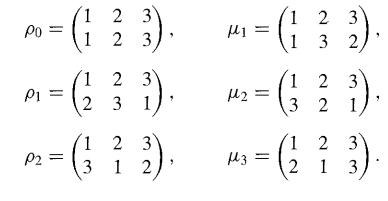
Step by Step Answer:






