Describe all subgroups of order ≤ 4 of Z₄ x Z₄, and in each case classify the factor group of Z₄ x Z₄ modulo the subgroup by Theorem 11.12. That is, describe the subgroup and say that the factor group of Z₄ x Z₄ modulo the subgroup is isomorphic to Z₂ x Z₄ , or whatever the case may be.

Data from Theorem 11.12

(Fundamental Theorem of Finitely Generated Abelian Groups) Every finitely generated abelian group G is isomorphic to a direct product of cyclic groups in the for

 

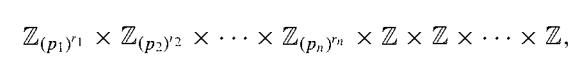
where the p_i are primes, not necessarily distinct, and the r_i are positive integers. The direct product is unique except for possible rearrangement of the factors; that is, the number (Betti number of G) of factors Z is unique and the prime powers (p_i )^ri are unique.

Proof: The proof is omitted here.

Transcribed Image Text:

Z(p₁)'¹ X Z(p2)'² X X Z(p) x Zxzx. x Z,