Deal with the concept of the torsion subgroup just defined.

An abelian group is torsion free if e is the only element of finite order. Use Theorem 11.12 to show that every finitely generated abelian group is the internal direct product of its torsion subgroup and of a torsion-free subgroup. (Note that {e} may be the torsion subgroup, and is also torsion free.) 

Data from Theorem 11.12

(Fundamental Theorem of Finitely Generated Abelian Groups) Every finitely generated abelian group G is isomorphic to a direct product of cyclic groups in the for

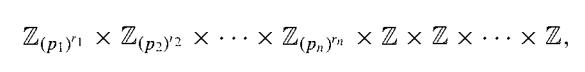
where the p_i are primes, not necessarily distinct, and the r_i are positive integers. The direct product is unique except for possible rearrangement of the factors; that is, the number (Betti number of G) of factors Z is unique and the prime powers (p_i )^ri are unique.

Proof: The proof is omitted here.

Transcribed Image Text:

Z(p₁)'¹ X Z(p2)'² X X Z(p) x Zxzx. x Z,