Give an example of an f(x) ∈ Q[x] that has no zeros in Q but whose zeros in C are all of multiplicity 2.
Explain how this is consistent with Theorem 51.13, which shows that Q is perfect.

Data from Theorem 51.13

Every field of characteristic zero is perfect.

Proof Let E be a finite extension of a field F of characteristic zero, and let α ∈ E. Then f(x) = irr(α, F) factors in F[x] into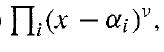 

where the α_i are the distinct zeros of irr(α, F), and, say, α= α₁. Thus

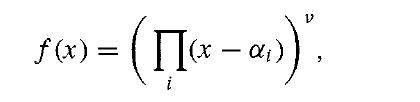
and since v · 1 ≠ 0 for a field F of characteristic 0, we must have

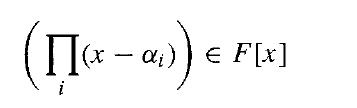
by Lemma 51.11. Since f(x) is irreducible and of minimal degree in F[x] having α as a zero, we then see that v = 1. Therefore, α is separable over F for all α ∈ E. By Corollary 51.10, this means that E is a separable extension of F.

Transcribed Image Text:

Π(x – α;)”,