In analogy with Examples 8.7 and 8.10, consider a regular plane n-gon for n 3. Each
Question:
In analogy with Examples 8.7 and 8.10, consider a regular plane n-gon for n ≥ 3. Each way that two copies of such an n-gon can be placed, with one covering the other, corresponds to a certain permutation of the vertices. The set of these permutations in a group, the nth dihedral group Dn• under permutation multiplication. Find the order of this group Dn. Argue geometrically that this group has a subgroup having just half as many elements as the whole group has.
Data from in example 8.7
An interesting example for us is the group S3 of 3! = 6 elements. Let the set A be { 1, 2, 3}. We list the permutations of A and assign to each a subscripted Greek letter for a name. The reasons for the choice of names will be clear later. Let
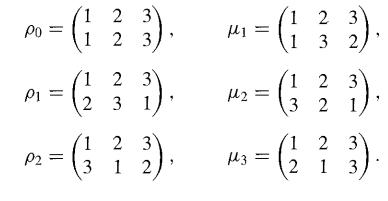
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





