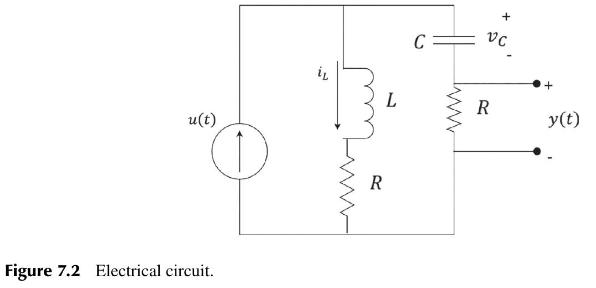
Consider the electrical circuit shown in Figure 7.2, where the input \(u(t)\) is a current and the output \(\mathbf{y}(\mathbf{t})\) is a voltage.

(a) Explain why the state variables should be chosen as \(x_{1}=i_{L}\) and \(x_{2}=v_{C}\).

(b) Write down state-variable equations for the system, and deduce the system's State-Space model \((A, B, C, D)\).

(c) Explain the concepts of controllability and observability. How are these properties determined for a system whose model is given by matrices \((A, B, C, D)\) ?

(d) In Figure 7.2, what conditions on R, \(L\) and \(C\) will guarantee that the system is: (i) controllable? (ii) observable?

(e) For the State-Space model derived in (b), if \(R=5 \Omega ; L=1 H\) and \(C=1 \mathrm{~F}\), design a block diagram for the circuit with one integrator for each state variable.

(f) Derive the circuit's transfer function using matrix algebra.

Transcribed Image Text:

u(t) Figure 7.2 Electrical circuit. iL www C + VC L R wwww R y(t)