Consider the electrical circuit in Figure 7.6, where the input \(u(t)\) is a voltage and the output \(y(t)\) is the total current flowing through the capacitor and inductor as indicated.

(a) Explain why the state variables should be chosen as \(x_{1}=v_{C}\) and \(x_{2}=i_{L}\).

(b) Write down state-variable equations for the system, and deduce the system's State-Space model \((A, B, C, D)\).

(c) Explain the concepts of controllability and observability. How are these properties determined for a system whose model is given by matrices \((A, B, C, D)\) ?

(d) What conditions relating \(R_{1}, R_{2}, L\) and \(C\) will render the system uncontrollable?

(e) What conditions relating \(R_{1}, R_{2}, L\) and \(C\) will render the system unobservable?

(f) For the State-Space model derived in (b), if \(R_{1}=R_{2}=5\) and \(L=C=1\), design a block diagram for the circuit with one integrator for each state variable.
(g) Derive the circuit's transfer function using matrix algebra.

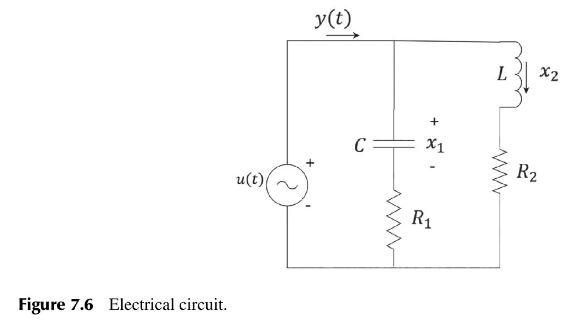
Figure 7.6 Electrical circuit. y(t) u(t)( + C + x1 R ww L R2 x2