In each of the following exercises use Corollary 17 .2 to work the problem, even though the answer might be obtained by more elementary methods. 

Find the number of orbits in {1, 2, 3, 4, 5, 6, 7, 8} under the cyclic subgroup ((1, 3, 5, 6)) of S₈.

Data from 17.2 Corollary 

If G is a finite group and X is a finite G-set, then number of orbits in X under G) 

 

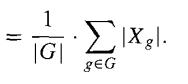
Proof:  The proof of this corollary follows immediately from the preceding theorem.

Transcribed Image Text:

1 |G| ΣΧ geG