In using the three isomorphism theorems, it is often necessary to know the actual correspondence given by the isomorphism and not just the fact that the groups are isomorphic. 

Repeat Exercise 5 for the group G = Z₃₆ with H = (9) and K = (18).

Data from Exercise 5

In the group G = Z₂₄, let H = (4) and K = (8). 

a. List the cosets in G/H, showing the elements in each coset. 

b. List the cosets in G/K, showing the elements in each coset. 

c. List the cosets in H/K, showing the elements in each coset. 

d. List the cosets in (G/K)/(H/K), showing the elements in each coset. 

e. Give the correspondence between G/ Hand (G/K)/(H/K) described in the proof of Theorem 34.7.

Data from Theorem 34.7

Let Hand K be normal subgroups of a group G with K ≤ H. Then G/H ≈ (G/K)/(H/K). 

Let ∅ : G → (G/K)/(H/K) be given by ∅(a)= (aK)(H/K) for a ∈ G. Clearly ∅ is onto (G/K)/(H/K), and for a, b ∈ G,

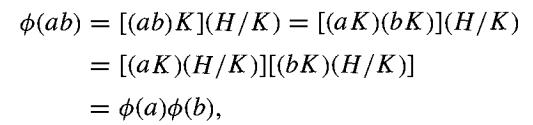
so ∅ is a homomorphism. The kernel consists of those x ∈ G such that ∅(x) = H/K. These x are just the elements of H. Then Theorem 34.2 shows that G/H ≈ (G/K)/(H/K).

p(ab) = [(ab)K](H/K) = [(aK)(bK)](H/K) = [(aK)(H/K)][(bK)(H/K)] = ()(b),