Let D 4 be the group of symmetries of the square in Example 8.10. a. Find the
Question:
Let D4 be the group of symmetries of the square in Example 8.10.
a. Find the decomposition of D4 into conjugate classes.
b. Write the class equation for D4 .
Data from Example 8.10
Let us form the dihedral group D4 of permutations corresponding to the ways that two copies of a square with vertices 1, 2, 3, and 4 can be placed, one covering the other with vertices on top of vertices (see Fig. 8.11). D4 will then be the group of symmetries of the square. It is also called the octic group. Again, we choose seemingly arbitrary notation that we shall explain later. Naively, we are using pi for rotations, µi for mirror images in perpendicular bisectors of sides, and δi for diagonal flips. There are eight permutations involved here. Let
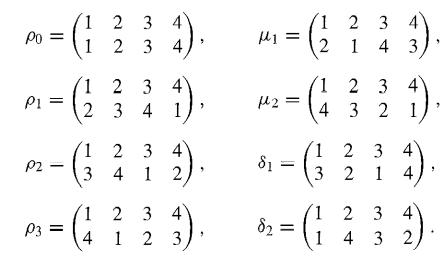
Step by Step Answer:






