Let F be an ordered field and let F ( (x)) be the field of formal Laurent

Question:

Let F be an ordered field and let F ( (x)) be the field of formal Laurent series with coefficients in F, discussed in Example 25.9. Describe the ordering of the monomials.• -x^-3, x^-2, x^-1, x⁰ = 1, x, x², x³, •••in the ordering of F((x)) described in that example.

Data from Example 25.9

(Formal Laurent Series Fields) continuing with the idea of Example 25.8, we let F be a field and consider formal series of the form ∑_i^∞_=N a_ixⁱ where N may be any integer, positive, zero, or negative, and a_i∈ F. (Equivalently, we could consider ∑_i^∞_{= -∞} a_ixⁱ where all but a finite number of the a_iare zero for negative values of i. In studying calculus for functions of a complex variable, one encounters series of this form called "Laurent series.") With the natural addition and multiplication of these series, we have a field which we denote by F((x)). The inverse of x is the series x^-1+ 0 + 0x + 0x² + • • •. Inverses of elements and quotients can be computed by series division. We compute three terms of (x^-1 - 1 + x - x² + x³ + •. •)/(x³ + 2x⁴ + 3x⁵ +•••)in R.((x)) for illustration.

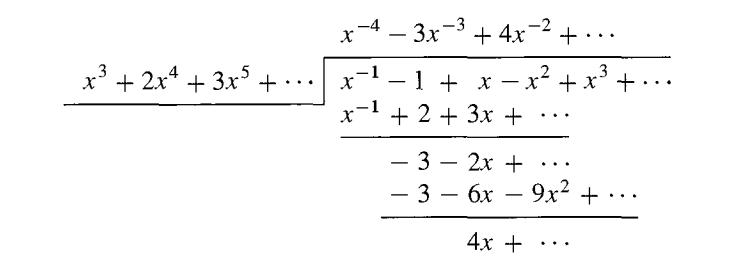
If F is an ordered field, we can use the obvious analog of P_low in R[[x]] to define an ordering of F((x)). In Exercise 2 we ask you to symbolically order the monomials • • • x^-3 , x^-2, x^-1, x⁰ = 1, x, x² , x³ , • • • as we did for R[x] in Example 25.6. Note that F((x)) contains, as a subfield, a field of quotients of F[x], and thus induces an ordering on this field of quotients.