let (Q((x)) have the ordering described in Example 25.9. List the labels a, b, c, d, e of the given elements in an order corresponding to increasing order of the elements as described by the relation < of Theorem 25.5. 

a 

b.

c.

d.

e. 4x 

Data from Example 25.9 

(Formal Laurent Series Fields) Continuing with the idea of Example 25.8, we let F be a field and consider formal series of the form ∑_i^∞_=N a_ixⁱ where N may be any integer, positive, zero, or negative, and a_i ∈ F. (Equivalently, we could consider ∑_i^∞_{= -∞} a_ixⁱ  where all but a finite number of the a_i are zero for negative values of i. In studying calculus for functions of a complex variable, one encounters series of this form called "Laurent series.") With the natural addition and multiplication of these series, we have a field which we denote by F((x)). The inverse of x is the series x^-1 + 0 + 0x + 0x² + • • •. Inverses of elements and quotients can be computed by series division. We compute three terms of (x^-1 - 1 + x - x² + x³ + •. •)/(x³ + 2x⁴ + 3x⁵ +•••)in R.((x)) for illustration.  

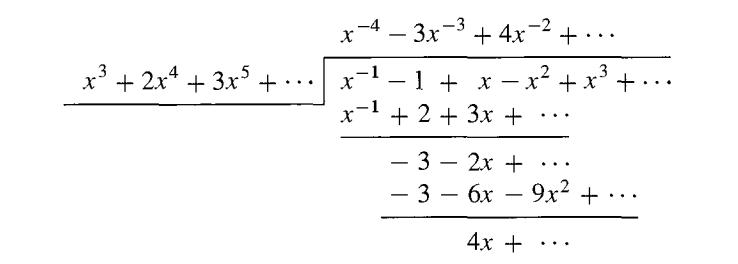
If F is an ordered field, we can use the obvious analog of P_low in R[[x]] to define an ordering of F((x)). In Exercise 2 we ask you to symbolically order the monomials • • • x^-3 , x^-2 , x^-1, x⁰ = 1, x, x² , x³ , • • • as we did for R[x] in Example 25.6. Note that F((x)) contains, as a subfield, a field of quotients of F[x ], and thus induces an ordering on this field of quotients.

Transcribed Image Text:

1 X