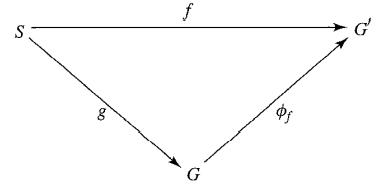
Let S be any set. A group G together with a fixed function g : S → G constitutes a blop group on S if for each group G' and map f : S → G' there exists a unique homomorphism ∅_f of G into G' such that f = ∅_f g (see Fig. 39.15). 

a. Let S be a fixed set. Show that if both G₁, together with g1 : S → G₁, and G₂, together with g₂ : S → G₂, are blop groups on S, then G₁ and G₂ are isomorphic. 

b. Let S be a set. Show that a blop group on Sexists. You may use any theorems of the text. 

c. What concept that we have introduced before corresponds to this idea of a blop group on S?

Figure

Transcribed Image Text:

S 8 09 f G Pf G