The sign of an even permutation is + 1 and the sign of an odd permutation is -1. Observe that the map sgn_n : S_n → {l, -1} defined by sgn_n(σ) = sign of σ is a homomorphism of S_n onto the multiplicative group { 1, -1}. What is the kernel? Compare with Example 13.3.

Data from example 13.3

13.3 Example: Let S_n be the symmetric group on n letters, and let ∅ : S_n → Z₂ be defined by

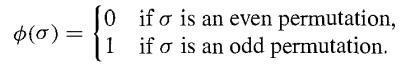
Show that ∅ is a homomorphism.

Solution: We must show that ∅(σµ) = ∅(σ) +∅(µ)for all choices of a,µ ∈ S_n. Note that the operation on the right-hand side of this equation is written additively since it takes place in the group Z₂. Verifying this equation amounts to checking just four cases: 

σ odd and µ odd, 

σ odd and µ even, 

σ even and µ odd, 

σ even and µ even. 

Checking the first case, if σ and µ can both be written as a product of an odd number of transpositions, then σµ can be written as the product of an even number of transpositions. Thus ∅(σµ)= 0 and ∅(σ) + ∅(µ)= 1 + 1 = 0 in Z₂. The other cases can be checked similarly.

Transcribed Image Text:

$(0) = (0 if o is an even permutation, if o is an odd permutation.