We consider the field E = Q(√2, √3, √5). It can be shown that [E : Q] = 8. In the notation of Theorem 48.3, we have the following conjugation isomorphisms (which are here automorphisms of E):

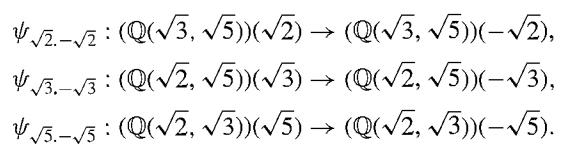
For shorter notation, let τ₂ = ψ_√2.-√2, τ₃ = ψ_{√3 -√3}, and , τ₅ = ψ_√5.-√5· Compute the indicated element of E. 

τ₂(√2 +√5)

Data from Theorem 48.3:

Let F be a field, and let α and β be algebraic over F with deg(α, F) = n. The map ψ_α.β :F(α) → F(β) defined by

for c_i ∈ F is an isomorphism of F(α) onto F(β) if and only if a and are conjugate over F.

2.-2 : (Q(3, 5))(2) (Q(3, 5))(-2), V3.-3: (Q(2, 5))(3) (Q(2, 5))(-3), 5.-5 : (Q(2, 3))(5) (Q(2, 3))(-5).