A uniform thin column of length L, positioned vertically with one end embedded in the ground, will deflect, or bend away, from the vertical under the influence of its own weight when its length or height exceeds a certain critical value. It can be shown that the angular deflection θ(x) of the column from the vertical at a point P(x) is a solution of the boundary-value problem:

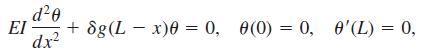
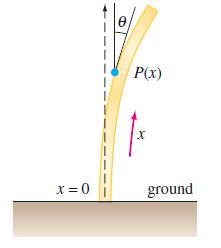
where E is Young’s modulus, I is the cross-sectional moment of inertia, δ is the constant linear density, and x is the distance along the column measured from its base. See Figure 6.4.7. The column will bend only for those values of L for which the boundary-value problem has a nontrivial solution.

(a) Restate the boundary-value problem by making the change of variables t = L -  x. Then use the results of a problem earlier in this exercise set to express the general solution of the differential equation in terms of Bessel functions.

(b) Use the general solution found in part (a) to find a solution of the BVP and an equation which defines the critical length L, that is, the smallest value of L for which the column will start to bend.

(c) With the aid of a CAS, find the critical length L of a solid steel rod of radius r = 0.05 in., δg = 0.28 A lb/in., E = 2.6 × 10⁷ lb/in.², A = πr², and I = 1/4πr⁴.

Transcribed Image Text:

EI dx² + 8g(L - x)0 = 0, 0(0) = 0, 0'(L) = 0,