Appropriately modify the procedure of Problem 68 to find a solution of

y'' + 3y' -  4y = 0,

y(0) = 0, y'(0) = 0, y''(0) = 1

Problem 68

In this problem you are led through the commands in Mathematica that enable you to obtain the symbolic Laplace transform of a differential equation and the solution of the initial-value problem by finding the inverse transform. In Mathematica the Laplace transform of a function y(t) is obtained using LaplaceTransform [y[t], t, s]. In line two of the syntax we replace LaplaceTransform [y[t], t, s] by the symbol Y. (If you do not have Mathematica, then adapt the given procedure by finding the cor esponding syntax for the CAS you have on hand.)

Consider the initial-value problem

y'' + 6y' + 9y = t sin t, y(0) = 2, y'(0) = -1.

Load the Laplace transform package. Precisely reproduce and then, in turn, execute each line in the following sequence of commands. Either copy the output by hand or print out the results.

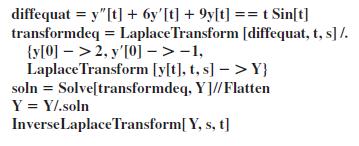2, y'[0] ->-1, Laplace Transform [y[t], t, s] - > Y} soln = Solve[transformdeq, Y]//Flatten Y = Y/.soln InverseLaplace Transform[ Y, s, t]" class="fr-fic fr-dii">

Transcribed Image Text:

diffequat = y"[t] + 6y'[t] + 9y[t] ==t Sin[t] transformdeq = Laplace Transform [diffequat, t, s]/. {y[0] – > 2, y'[0] ->-1, Laplace Transform [y[t], t, s] - > Y} soln = Solve[transformdeq, Y]//Flatten Y = Y/.soln InverseLaplace Transform[ Y, s, t]