As was mentioned in Problem 22, the differential equation (5) that governs the deflection y(x) of a
Question:
As was mentioned in Problem 22, the differential equation (5) that governs the deflection y(x) of a thin elastic column subject to a constant compressive axial force P is valid only when the ends of the column are hinged. In general, the differential equation governing the deflection of the column is given by

Assume that the column is uniform (EI is a constant) and that the ends of the column are hinged. Show that the solution of this fourth-order differential equation subject to the boundary conditions y(0) = 0, y''(0) = 0, y(L) = 0, y''(L) = 0 is equivalent to the analysis in Example 4.
Problem 22
The critical loads of thin columns depend on the end conditions of the column. The value of the Euler load P1 in Example 4 was derived under the assumption that the column was hinged at both ends. Suppose that a thin vertical homogeneous column is embedded at its base (x = 0) and free at its top (x = L) and that a constant axial load P is applied to its free end. This load either causes a small deflection d as shown in Figure 5.2.9 or does not cause such a deflection. In either case the differential equation for the deflection y(x) is
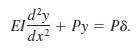

Step by Step Answer:

A First Course in Differential Equations with Modeling Applications
ISBN: 978-1111827052
10th edition
Authors: Dennis G. Zill





