Consider a pendulum that is released from rest from an initial displacement of 0 radians. Solving

Consider a pendulum that is released from rest from an initial displacement of θ₀ radians. Solving the linear model (7) subject to the initial conditions θ(0) = θ₀, θ'(0) = 0 gives θ(t) = θ₀ cos √g/lt. The period of oscillations predicted by this model is given by the familiar formula Y = 3π/√g/l = 2π√l/g.. The interesting thing about this formula for T is that it does not depend on the magnitude of the initial displacement θ₀. In other words, the linear model predicts that the time it would take the pendulum to swing from an initial displacement of, say, θ₀ = π/2 (= 90°) to –π/2 and back again would be exactly the same as the time it would take to cycle from, say, θ₀ = π/360 (= 0.5°) to –π/360. This is intuitively unreasonable; the actual period must depend on θ₀.

If we assume that g = 32 ft/s² and l = 32 ft, then the period of oscillation of the linear model is T = 2π s. Let us compare this last number with the period predicted by the nonlinear model when θ₀ = π/4. Using a numerical solver that is capable of generating hard data, approximate the solution of

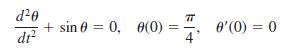
on the interval 0 ≤ t ≤ 2. As in Problem 25, if t1 denotes the first time the pendulum reaches the position OP in Figure 5.3.3, then the period of the nonlinear pendulum is 4t₁. Here is another way of solving the equation θ(t) = 0. Experiment with small step sizes and advance the time, starting at t = 0 and ending at t = 2. From your hard data observe the time t₁ when θ(t) changes, for the first time, from positive to negative. Use the value t₁ to determine the true value of the period of the nonlinear pendulum. Compute the percentage relative error in the period estimated by T = 2π.

Transcribed Image Text:

d20 + sin 0 = 0, 0(0) = dr O'(0) = 0 4' %3D