Solving a nonhomogeneous linear system X' = AX + F(t) by variation of parameters when A is a 3 × 3 (or larger) matrix is almost an impossible task to do by hand. Consider the system

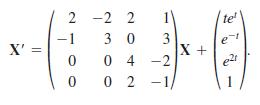
(a) Use a CAS or linear algebra software to find the eigenvalues and eigenvectors of the coefficient matrix.

(b) Form a fundamental matrix φ(t) and use the computer to find φ^-1(t).

(c) Use the computer to carry out the computations of:

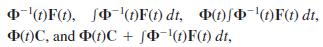
where C is a column matrix of constants c₁, c₂, c₃, and c₄.

(d) Rewrite the computer output for the general solution of the system in the form X = X_c + X_p, where X_c = c₁X₁ + c₂X₂ + c₃X₃ + c₄X₄.

-)F(t), JO)F(t) dt, (t)f )F(t) dt, D(t)C, and (t)C + j()F(t) dt,