The differential equation y'' - 2xy' + 2y = 0 is known as Hermites equation of order

Question:

The differential equation

y'' - 2xy' + 2αy = 0

is known as Hermite’s equation of order α after the French mathematician Charles Hermite (1822-1901). Show that the general solution of the equation is y(x) = c₀y₁(x), + c₁y₂(x), where

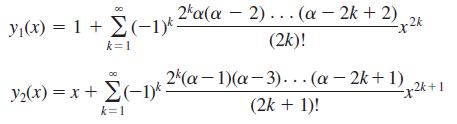
24a(a - 2)... (a - 2k + 2) 2k y(x) = 1 + (-1)* (2k)! k=1 2 (a-1)(a-3).. .(a- 2k+ 1) 2k+1 y2(x) = x + E(-1)* (2k + 1)! k=1

are power series solutions centered at the ordinary point 0.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

A First Course in Differential Equations with Modeling Applications

ISBN: 978-1111827052

10th edition

Authors: Dennis G. Zill

See More Books

Question Posted: Oct 29, 2020 08:53 AM

See More Questions

Find the solution set of the system of linear equations represented by the augmented matrix: 1 2 4 0 2 -4 0 0 0 0.0 (c) 5 -1 7 1 (a) 0 0 0 -10 (b) 1 0 1 0 0 0 00 0 0 0 0
The Laplace transform, named after the French mathematician Pierre-Simon de Laplace (1749-1827), of a function f(x) is given by L{f(t)}(s) = Laplace transforms are useful for solving differential...
Note that x = 0 is an ordinary point of the differential equation y'' + x 2 y' + 2xy = 5 2x + 10x 3 . Use the assumption
Products are 1. Lip gloss or lipstick with SPF 2. Custom facial sheets you can make online or in store pickup and have it send to your home based on your needs 3. A foundation sunscreen Price Provide...
Let xn := 1/12 + 1/22 + +1/n2 for each n N. Prove that (xn) is increasing and bounded, and hence converges. [If k > 2, then 1/k2 1/k(k - 1) = 1/(k - 1) - 1/k.]
for a better way to do this comparison, which pays proper attention to statistical-analysis issues.
15. The profit calculation in the chapter assumes that you borrow at a fixed interest rate to finance investments. An alternative way to borrow is to short-sell stock. What complications would arise...
Suppose a new process was developed that could be used to make oil out of seawater. The equipment required is quite expensive; but it would, in time, lead to low prices for gasoline, electricity, and...
Required: 1-a. Compute the predetermined overhead rate using direct labor-hours as the basis for allocating overhead costs to products. 1-b. Compute the unit product cost for one unit of each model....
The development manager of a website for online book-buying has asked you to carry out a heuristic evaluation of its usability. He has specifically proposed the three heuristics listed below. 1....
Use a root-finding application to find the zeros of P 1 (x), P 2 (x), . . . , P 7 (x). If the Legendre polynomials are built-in functions of your CAS, find zeros of Legendre polynomials of higher...
(a) When = n is a nonnegative integer, Hermites differential equation always possesses a polynomial solution of degree n. Use y 1 (x), given in Problem 51, to find polynomial solutions for n = 0, n...
In Exercises 3150, find f + g, f - g, fg, and f/g. Determine the domain for each function. f(x) = 2x + 3, g(x) = x - 1
The accountant at EZ Toys, Inc. is analyzing the production and cost data for its Trucks Division. For October, the actual results and the master budget data are presented below. Actual Results:...
2. 2D Design (4 points): The Pawnee Department of Parks and Recreation has received alarming reports that their picnic tables might be unstable. Examine the picnic table design below (which weighs 50...
Answer 3-10 Cash flow Bailey Corporations income statement (dollars are in thousands) is given here: Sales Operating costs excluding depreciation $14,000,000 and amortization EBITDA Depreciation and...
You want to create a database for computer lab management. You want to keep track of the following information (Type your answer): The information about computer/workstation such as station ID,...
You have been hired for a newly created position for a large medical office that employs five MDs and four Advanced Practice Registered Nurses (APRNs). Upper leadership created this position due to...
You bought one of Elkins Manufacturing Co.s 5.4 percent coupon bonds one year ago for $1,030. These bonds make annual payments, mature eight years from now, and have a par value of $1,000. Suppose...
Complete the following acid-base reactions: (a) HCCH + NaH
What is the probability that exactly two of the two offspring will be affected in a family with dominant disease with reduced penetrance? Genetics A dominantly inherited genetic disease is identified...
What is the probability that the mode of transmission for this particular family is dominant with complete penetrance? Is this a prior probability or a posterior probability? Genetics A dominantly...
Suppose you are a genetic counselor and are asked by the parents what the probability is that if they have another (a third) child he or she will be affected by the disease. What is the answer?...
Los datos de la columna C tienen caracteres no imprimibles antes y despus de los datos contenidos en cada celda. En la celda G2, ingrese una frmula para eliminar cualquier carcter no imprimible de la...
Explain impacts of changing FIFO method to weighted average method in inventory cost valuations? Explain impacts of changing Weighted average method to FIFO method in inventory cost valuations?...
A perpetuity makes payments starting five years from today. The first payment is 1000 and each payment thereafter increases by k (in %) (which is less than the effective annual interest rate) per...

The differential equation y'' - 2xy' + 2y = 0 is known as Hermites equation of order

Question:

24a(a - 2)... (a - 2k + 2) 2k y(x) = 1 + (-1)* (2k)! k=1 2 (a-1)(a-3).. .(a- 2k+ 1) 2k+1 y2(x) = x + E(-1)* (2k + 1)! k=1

Step by Step Answer:

A First Course in Differential Equations with Modeling Applications

Students also viewed these Mathematics questions