Consider the models W l 2 g and W g 3 . Interpret each of
Question:
Consider the models W ∝ l2g and W ∝ g3. Interpret each of these models geometrically. Explain how these two models differ from Models (2.11) and (2.13), respectively. In what circumstances, if any, would the four models coincide? Which model do you think would do the best job of predicting W? Why? In Chapter 3 you will be asked to compare the four models analytically.
a. Let A (x) denote a typical cross-sectional area of a bass, 0 ≤ x ≤ l, where l denotes the length of the fish. Use the mean value theorem from calculus to show that the
volume V of the fish is given by:
![]()
where A̅ is the average value of A(x).
b. Assuming that A̅ is proportional to the square of the girth g and that weight density for the bass is constant, establish that:
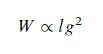
Data from model 2.11
Let's accept the model, at least for further testing, based on the small amount of data presented so far. Because the data point (14.53; 26) lies along the line we have drawn in Figure 2.20, we can estimate the slope of the line as 26/3049 = 0.00853, yielding the model:

Data from model 2.13
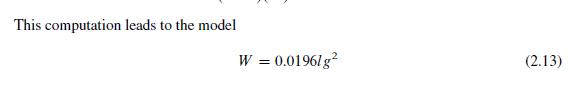
Step by Step Answer:

A First Course In Mathematical Modeling
ISBN: 9781285050904
5th Edition
Authors: Frank R. Giordano, William P. Fox, Steven B. Horton





