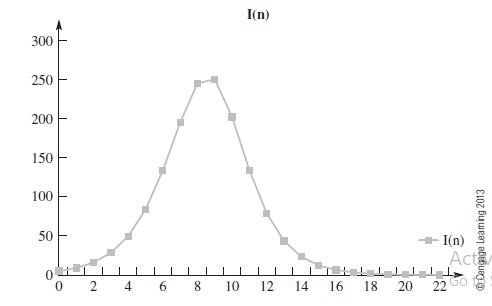
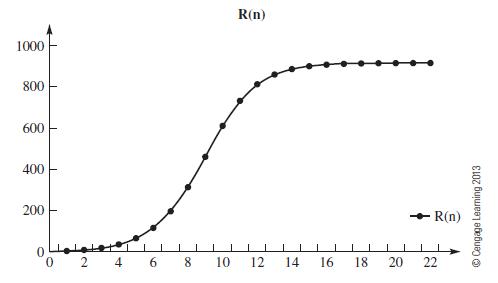
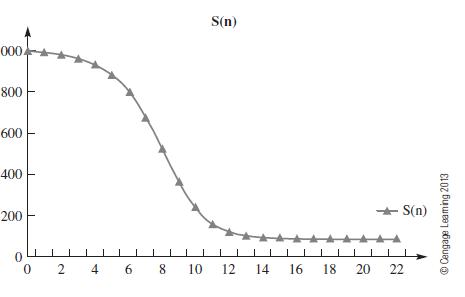
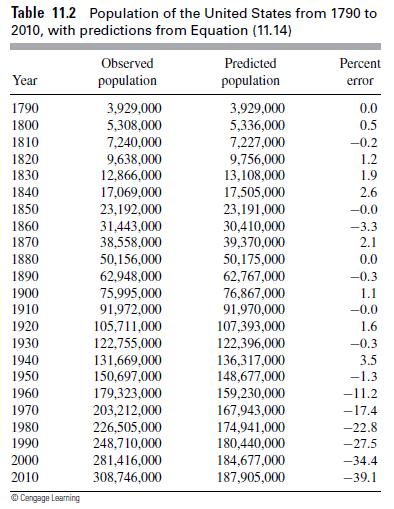
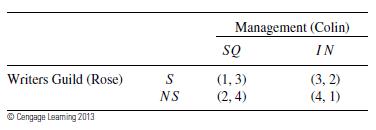
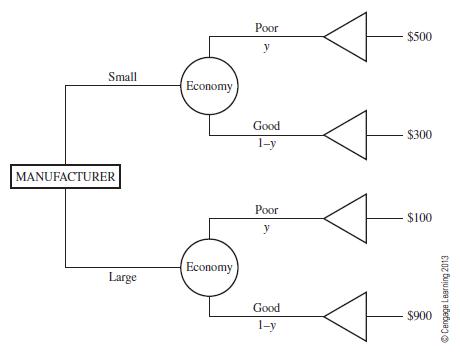
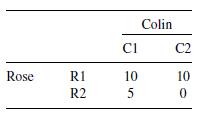
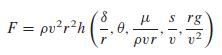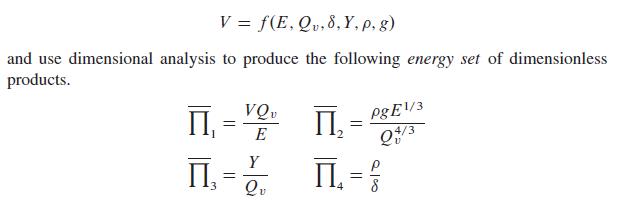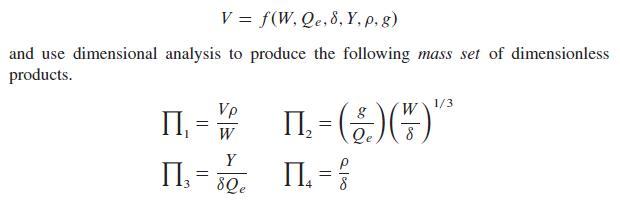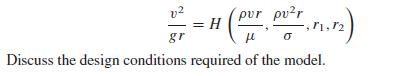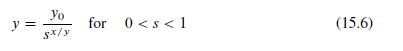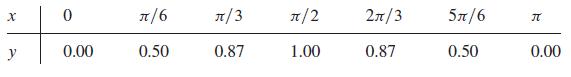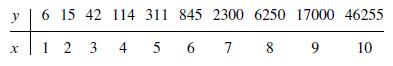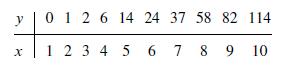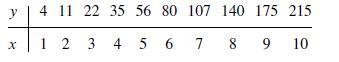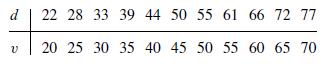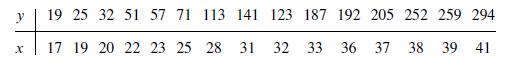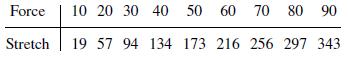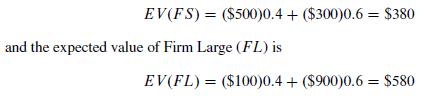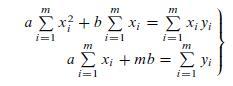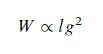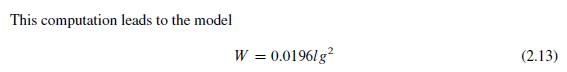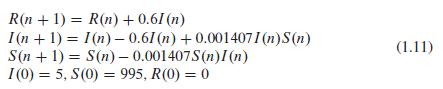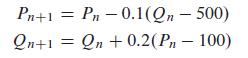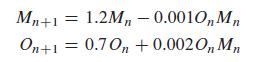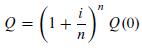A First Course In Mathematical Modeling 5th Edition Frank R. Giordano, William P. Fox, Steven B. Horton - Solutions
Discover a comprehensive resource for "A First Course In Mathematical Modeling 5th Edition" by Frank R. Giordano, William P. Fox, and Steven B. Horton. Access online answers and a solution manual that includes detailed solutions PDF, offering step-by-step answers to complex problems. Whether you're looking for a test bank, instructor manual, or chapter solutions, this textbook provides it all. Benefit from solved problems and questions and answers that enhance your understanding. Enjoy the convenience of a free download to support your studies and excel in mathematical modeling.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


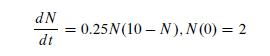


![-(u(x) [y(x) - y(x)]) = 0 dx Conclude that u(x)[y (x) - y(x)] = constant.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/4/6/2/571659808eb4484a1704462569699.jpg)
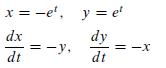
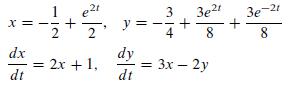
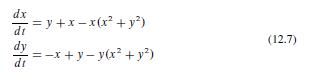


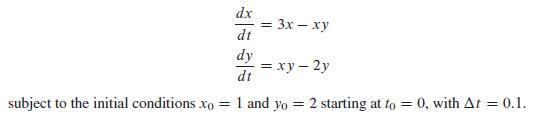
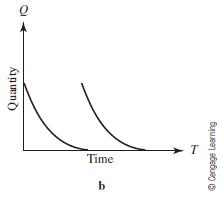
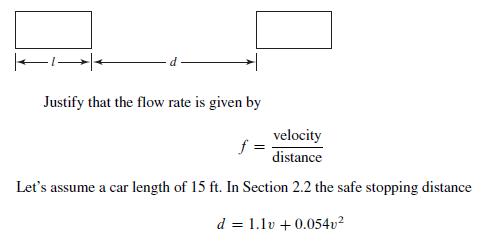

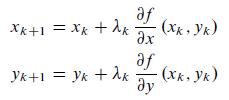
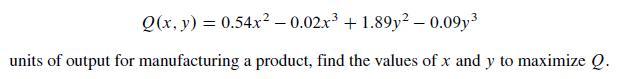
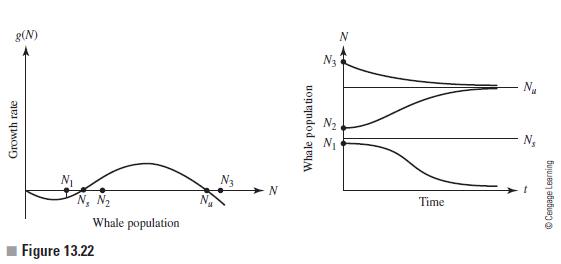

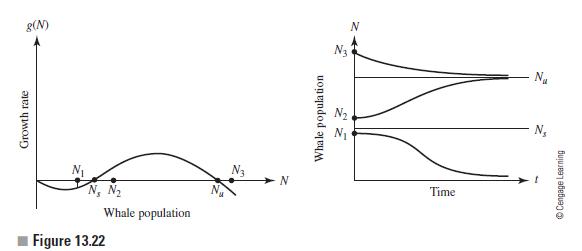
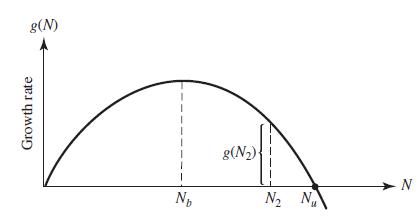
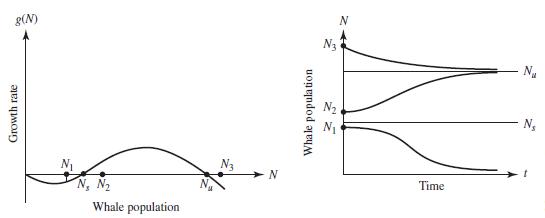
![TP = g(N) [p-c(N)] (13.8)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1706/0/1/5/62765afbb8b055bb1706015625853.jpg)