Consider Example 1, A Car Rental Company. Experiment with different values for the coefficients. Iterate the resulting dynamical system for the given initial values. Then experiment with different starting values. Do your experimental results indicate that the model is sensitive:

a. To the coefficients?

b. To the starting values?

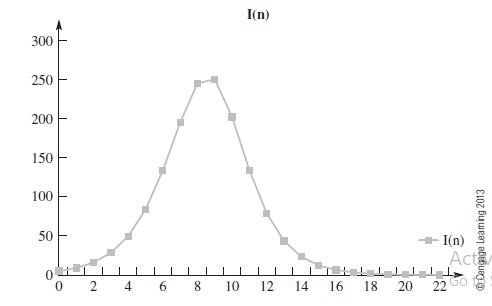
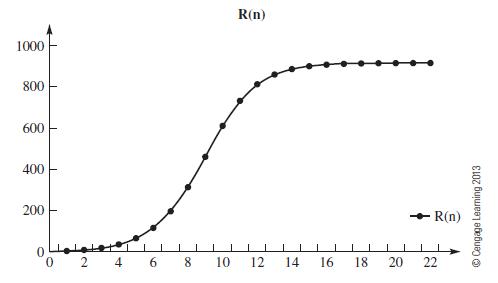
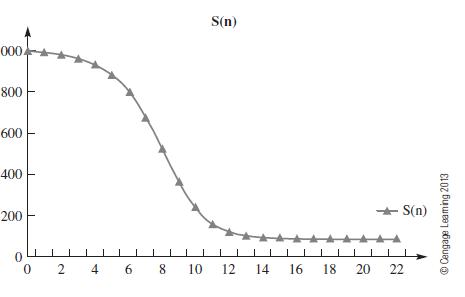
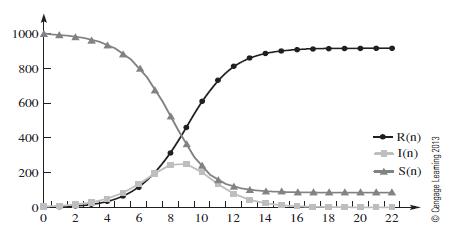
Data from example 1

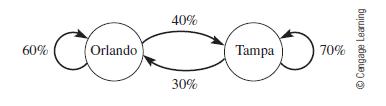
A car rental company has distributorships in Orlando and Tampa. The company specializes in catering to travel agents who want to arrange tourist activities in both cities. Consequently, a traveler will rent a car in one city and drop the car off in the second city. Travelers may begin their itinerary in either city. The company wants to determine how much to charge for this drop-off convenience. Because cars are dropped off in both cities, will a sufficient number of cars end up in each city to satisfy the demand for cars in that city? If not, how many cars must the company transport from Orlando to Tampa or from Tampa to Orlando? The answers to these questions will help the company figure out its expected costs. The historical records reveal that 60% of the cars rented in Orlando are returned to Orlando, whereas 40% end up in Tampa. Of the cars rented from the Tampa office, 70% are returned to Tampa, whereas 30% end up in Orlando. Figure 1.22 is helpful in summarizing the situation.

Figure 1.22

Dynamical Systems Model Let's develop a model of the system. Let n represent the number of business days. Now define:
O_n = the number of cars in Orlando at the end of day n T_n = the number of cars in Tampa at the end of day n Thus the historical records reveal the system:

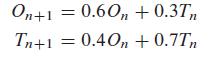
Equilibrium Values The equilibrium values for the system are those values of On and T_n for which no change in the system takes place. Let's call the equilibrium values, if they exist, O and T, respectively. Then O = O_n+1 = O_n and T = T_n+1 = T_n simultaneously. Substitution in our model yields the following requirements for the equilibrium values:

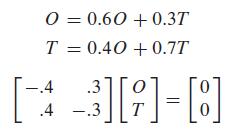
This system is satisfied whenever O = 3/4T. For example, if the company owns 7000 cars and starts with 3000 in Orlando and 4000 in Tampa, then our model predicts that:

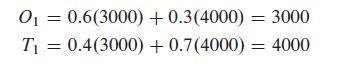
Thus, this system remains at (O, T) = (3000, 4000) if we start there. Next let's explore what happens if we start at values other than the equilibrium values. Let's iterate the system for the following four initial conditions:

A numerical solution, or table of values, for each of the starting values is graphed in Figure 1.23.

Figure 1.23

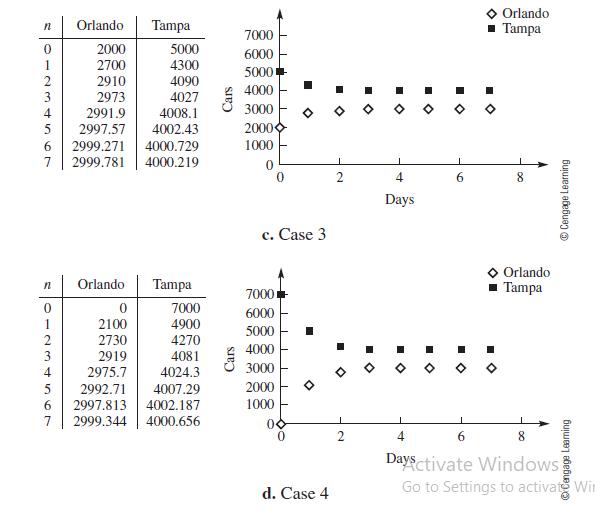
Sensitivity to Initial Conditions and Long-Term Behavior In each of the four cases, within a week the system is very close to the equilibrium value (3000; 4000) even in the absence of any cars at one of the two sites. Our results suggest that the equilibrium value is stable and insensitive to the starting values. Based on these explorations, we are inclined to predict that the system approaches the equilibrium where 3/7 of the fleet ends up in Orlando and the remaining 4/7 in Tampa. This information is helpful to the company. Knowing the demand patterns in each city, the company can estimate how many cars it needs to ship. In the problem set; we ask you to explore the system to determine whether it is sensitive to the coefficients in the equations for O_n+1 and T_n+1.

Transcribed Image Text:

300 250 200 150 100 50 T T T 0 2 4 9. 6 8 I(n) 10 12 14 16 18 20 I(n) Cengage Leaming 2013 Act 22 GO