Question: Write a computer code to perform the gradient method of steepest ascent algorithm using the Golden Section Search Method (presented in Section 7.6) to maximize
Write a computer code to perform the gradient method of steepest ascent algorithm
using the Golden Section Search Method (presented in Section 7.6) to maximize the
function:
![]()
to obtain λ=λk at each step determining the next point (xk+1, yk+1) in Equations (13.4).
Use your code to solve Problems 6 and 7 of this section.
Equation 13.4
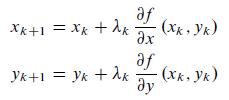
Data from problem 6
If x and y are the amounts of labor and capital, respectively, to produce:
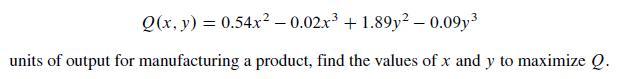
Data from problem 7
The total cost to manufacture one unit of product A is $3, and for one unit of product B it is $2. If x and y are the retail prices per unit of A and B, respectively, then marketing research has established that:
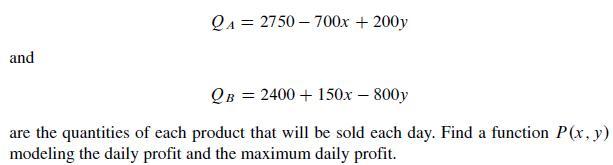
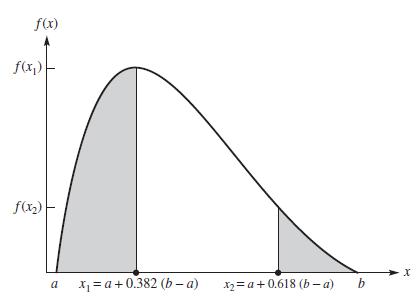
Data from section 7.6

Figure 7.24
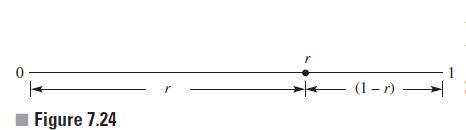

![Only the positive root r lies in the given interval [0, 1]. The numerical value of ris approximately 0.618](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1706/0/1/7/72265afc3ba0a5bb1706017720544.jpg)

g() = f(xk + XVf(xk))
Step by Step Solution
3.48 Rating (161 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


