For the differential equation model obtained in Problem 5, find Q(t) by separating the variables and integrating.

a. Evaluate Q (1).

b. Compare your previous estimates of Q (1) with its actual value.

c. Find the effective annual interest rate when an annual rate of 10% is compounded continuously.

d. Compare the effective annual interest rate computed in part (c) with interest compounded.

i.

ii.

iii.

iv.

Data from problem 5

When interest is compounded, the interest earned is added to the principal amount so that it may also earn interest. For a 1-year period, the principal amount Q is given by:

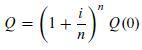
where i is the annual interest rate (given as a decimal) and n is the number of times during the year that the interest is compounded. To lure depositors, banks offer to compound interest at different intervals: semiannually, quarterly, or daily. A certain bank advertises that it compounds interest continuously. If $100 is deposited initially, formulate a mathematical model describing the growth of the initial deposit during the first year. Assume an annual interest rate of 10%.

Semiannually: (1 + 0.1/2)