Refer to Example 1; formulate and then solve both the firm's game and the economy's game algebraically.

Data from example 1

Let's consider the following scenario. A manufacturing firm is considering whether to gear  for a small production or a large production. The firm plans to implement a decision that will be executed for a period of the next several years. The economy (nature) may be poor or good during the period being studied. Let's assume that the net profits in hundreds of thousands of dollars have been projected by the firm's economists as follows:

We could consider this as a one-player decision as we did in Chapter 9 using a decision tree and make assumptions concerning the probability or a poor economy y and a good economy, (1 –y). This is shown in Figure 10.23.

Figure 10.23

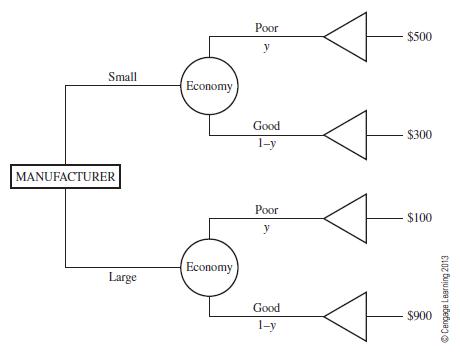
For example, if the probability of a poor economy is y = 0.4, then the expected value of Firm Small (FS) is:

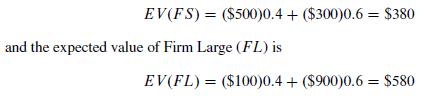
Under these assumptions, the firm should implement the Firm Large strategy and average $580,000.  Now let's consider the firm's decision as a game against nature, the economy. First, let's find a strategy for the firm that guarantees an outcome regardless of what the economy does.

The Firm's Game We define V Net profit in hundreds of thousands of dollars x Portion of the time that the firm should play Firm Small (FS) (1– x) Portion the firm should play Firm Large (FL) First, the Economy could play a pure Economy Poor (EP) strategy against the firm's mixed strategy, giving an expected value that represents an upper limit on the profit the firm can make.

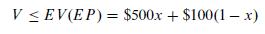
Next, the Economy could play a pure Economy Good (EG) strategy against the firm's mixed strategy, giving an expected value that again represents an upper limit on the profit the firm can make.

The geometric solution to the linear program is given in Figure 10.24.

Figure 10.24

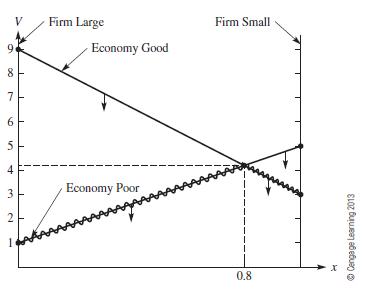We estimate the solution as (0.8, $420), giving the strategy for the firm as 80% Firm Small, 20% Firm Large. Thus, if the rm plays a mixed strategy of 80% Small, 20% Large, its net profit will be $420,000 regardless of whether the economy is always poor, always good, or any mix of poor and good. At this point, the rm has a conservative strategy that guarantees $420,000. Now let's consider the game from the economy's perspective.

The Economy's Game What is the worst that the economy could do to the manufacturer?We define the following variables:
V = Net profit in hundreds of thousands of dollars y = Portion of the time that the economy should play Economy Poor (EP) (1 –y) = Portion of the time that the economy should play Economy Good (EG) First, the Firm could play a pure Firm Small (FS) strategy against the economy's mixed strategy, giving an expected value that represents a lower limit on the ability of the economy to limit the firm.

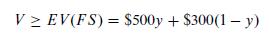
Next, the Firm could play a pure Firm Large (FL) strategy against the economy's mixed strategy, giving an expected value that again represents a lower limit on the ability of the economy to limit the firm's profit.

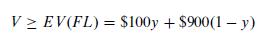
Since y is a probability, y is constrained to the interval 0 ≤ y ≤1, giving the linear program for the economy's decision:

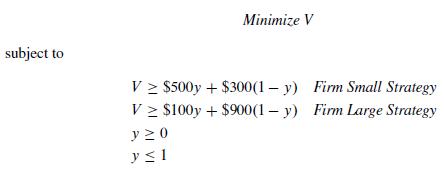
The geometric solution to the linear program is given in Figure 10.25. We estimate the solution as (0.6, $420), giving the strategy for the economy as 60% Poor, 40% Good. To minimize the firm's profit, the economy should be poor 60% of the time. If so, the economy could limit the firm to a profit of $420,000. Now, the firm can use both the firm's game and the economy's game to define several options. If the firm were uncertain about the economy, the firm could play its conservative strategy of 80% Small and 20% Large to guarantee $420,000. However, from the economy's game, if the firm thought the economy would be poor more than 60% of the time, the firm should employ its small strategy and make more than $420,000. If the rm believes the economy will be poor less than 60% of the time, it should employ its large strategy to again make more than the $420,000 as Figure 10.24 suggests.

Figure 10.25

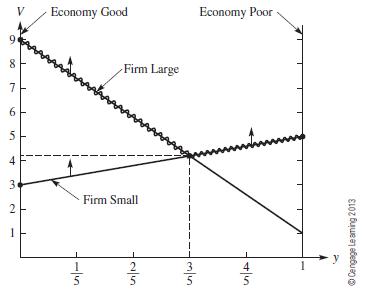
Figure 10.24

Summarizing, the combination of the analyses from both the firm's perspective and the economy's perspective allows the rm to make a conservative decision to play a mixed strategy and be guaranteed a net profit of $420,000 or make a speculative decision by betting on whether the economy will be poor more or less than 60% of the time and playing the appropriate pure strategy, Firm Small or Firm Large. While the economy is not a reasoning player, it is advantageous to know what its optimal strategy is. In the exercises, you are asked to derive the solutions for both the firm and the economy algebraically. While we considered only two strategies for the firm and two for the economy, larger problems are easily formulated and solved using linear programming, as suggested in the exercises.

Transcribed Image Text:

Firm Small Large Nature: Economy Good $300 Poor $500 $100 $900