In Example 4, Travelers' Tendencies at a Regional Airport, experiment with starting values near the origin. Does the origin appear to be a stable equilibrium? Explain.

Experiment with different values for the coefficients using the starting values given. Then try different starting values. What is the long-term behavior? Do your experimental results indicate the model is sensitive to the coefficients? To the starting values? Now assume that each airlines recruits new travelers. Initially assume that the total number of travelers increases as each airlines recruits new travelers. Experiment with different starting values for new travelers. What is the long-term behavior? Does it seem to be sensitive to the rate of recruiting new travelers? How would you adjust your model to reflect the total number of travelers in the region as a constant. Adjust your model to reflect what is happening at your closest airport. What do you think will happen at your closest airport in the long haul?

Data from example 4

Consider a regional airport that is supported by three major airlines: American Airlines, United Airlines, and US Airways, each flying out to respective hubs. We survey the weekly local business travelers and find 75% of those who traveled on US Airways traveled again on US Airways, 5% switched to fly United, and 20% switched to fly American. Of those who traveled on United, 60% traveled again on United, but 20% switched to US Airways, and 20% switched to American. Of those who traveled on American, only 40% remained with American, 40% switched to US Airways, and 20% switched to United. We assume these tendencies continue week to week and that no additional local business travelers enter or leave the system. These tendencies are depicted in Figure 1.29.

Figure 1.29

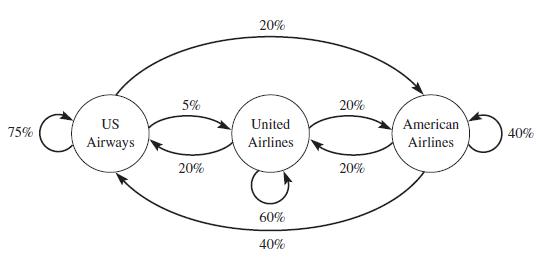
To formulate a system of difference equations, let n represent the nth week of traveling and define:

S_n = the number of US Airways travelers in week n
U_n = the number of United Airlines travelers in week n
A_n = the number of American Airlines travelers in week n

Formulating the system of difference equations, we have the following dynamical system:

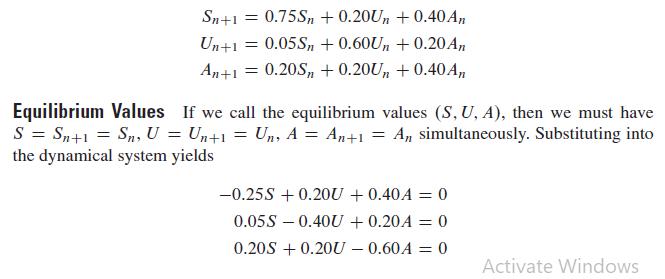
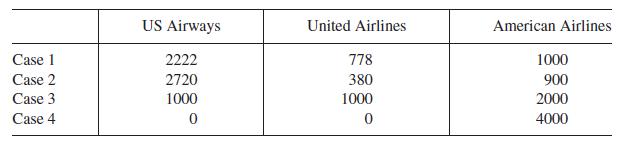
There are an infinite number of solutions to this system of equations. Letting A = 1, we find the system is satisfied when S = 2.2221 and U = 0.7777694 (approximately). Suppose the system has 4000 weekly travelers. Then, S = 2222, U = 778, and A = 1000 travelers should approximate the equilibrium values. Let's use a spreadsheet to check the equilibrium values and several other values. The total number of travelers in the system is 4,000 with initial travelers as follows:

The numerical solutions for the starting values are graphed in Figure 1.30.

Figure 1.30

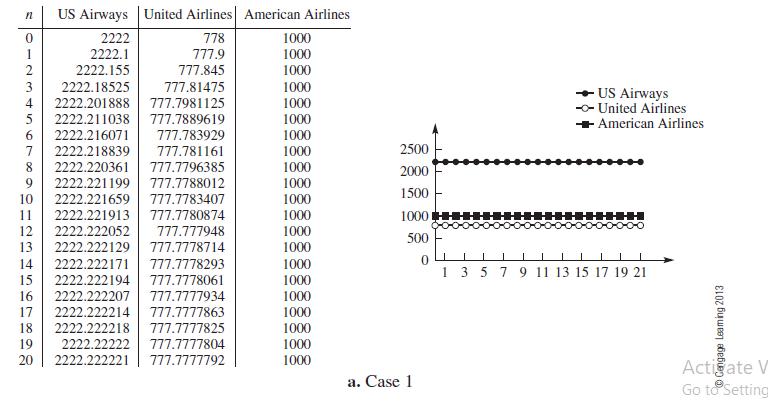
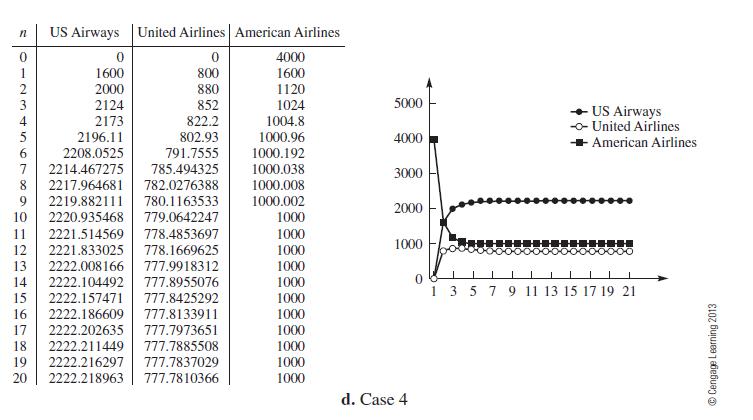
Sensitivity to Initial Conditions and Long-Term Behavior Suppose initially there are 4000 travelers in the system, and all remain in the system. At least for the starting values that we investigated, the system approaches the same result, even if initially there are no travelers traveling US Airways or United Airlines in the system. The equilibrium investigated appears to be stable. Starting values in the vicinity of the equilibrium appear to approach the equilibrium. What about the origin? Is it stable? In the problem set, you are asked to explore this system further by examining other starting values and changing the coefficients of the model. Additionally, you are asked to investigate systems in which the travelers enter and leave the system.

Transcribed Image Text:

75% US Airways 5% 20% 20% United Airlines 60% 40% 20% 20% American Airlines 40%