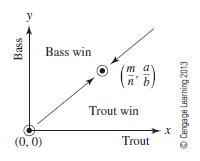
Show that the two trajectories leading to (m, a/b) shown in Figure 12.8 are unique.

Figure 12.8

a. From system (12.6) derives the following equation:

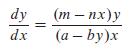
b. Separate variables, integrate, and exponentiate to obtain:

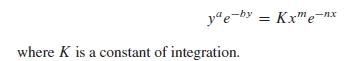
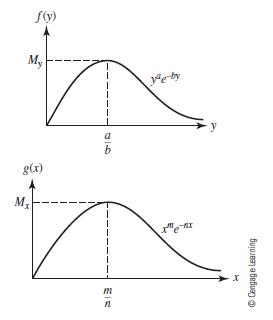
c. Let f (y) = y ^a/ e ^by and g(x) = x ^m/e ^nx. Show that f (y) has a unique maximum of
M_y = (a/eb)^a when y = a/b as shown in Figure 12.12. Similarly, show that g(x)
has a unique maximum M_x = (x/en) ^m when x = m, also shown in Figure 12.12.

Figure 12.12

d. Consider what happens as (x, y) approaches (m, a/b) Take limits in part (b) as x → m and y → a/b to show that:

e. Show that only one trajectory can approach (m, a/b) from below the line y = a/b. Pick y₀ 0) y, which implies that:

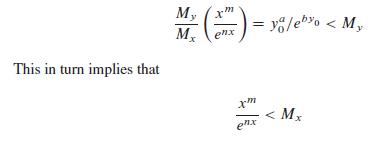
Figure 12.12 tells you that for g(x) there is a unique value x₀ 

Figure 12.13

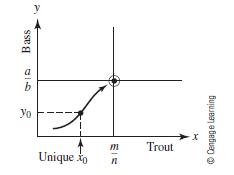
f. Use a similar argument to show that the solution trajectory leading to (m, a/b) is unique if y₀ > a/b.

Transcribed Image Text:

Bass y (0,0) Bass win m Trout win Trout Cengage Learning 2013