Let (X, Y) be uniformly distributed in the circle of radius 1 centered at the origin. Its joint density is thus

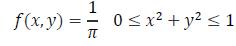
Let R = (X² + Y²)^1/2 and θ = tan^-1(Y/X) denote the polar coordinates of (X, Y). Show that R and θ are independent, with R² being uniform on (0, 1) and θ being uniform on (0, 2π).

Transcribed Image Text:

1 f(x, y) 0sx² + y2 < 1