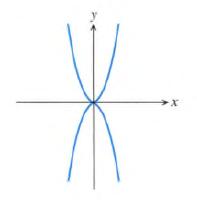
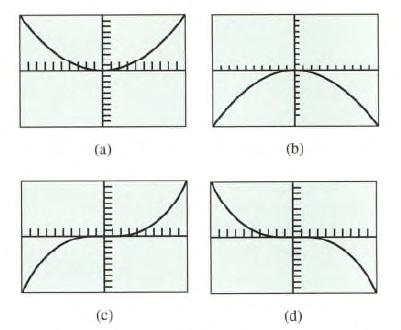
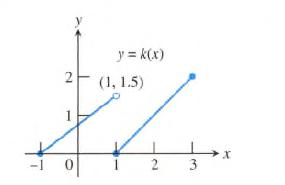
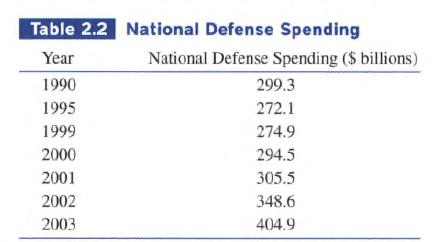
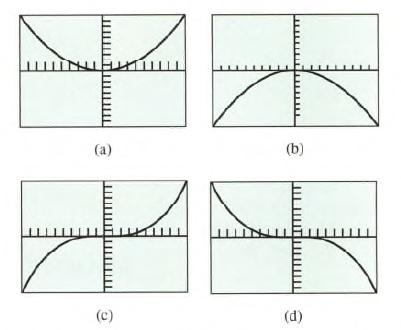
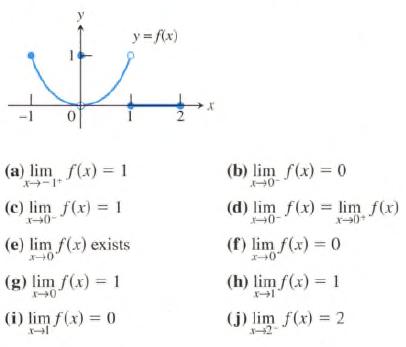
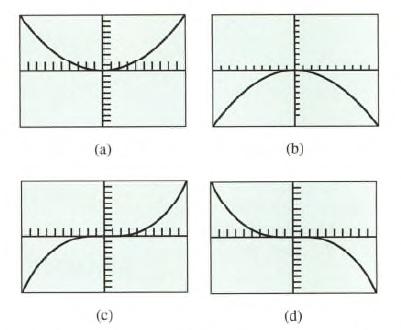
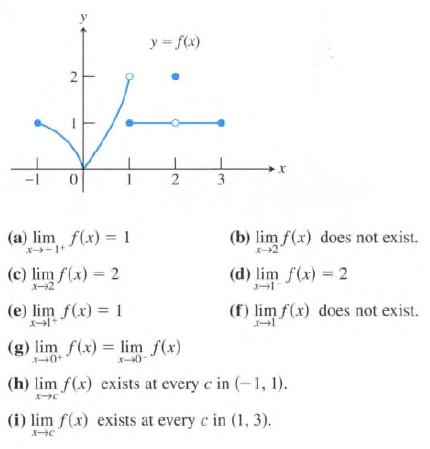
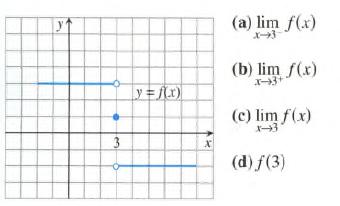
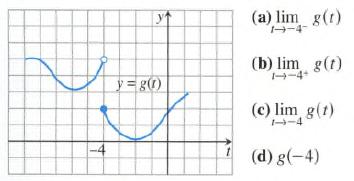
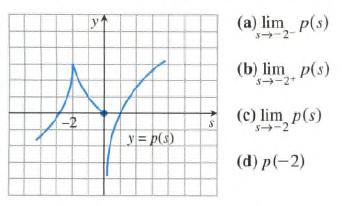
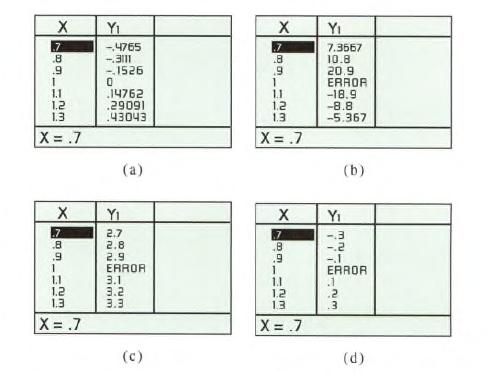
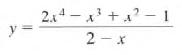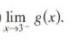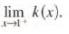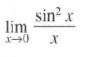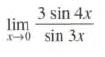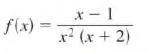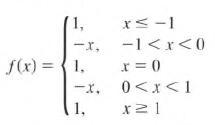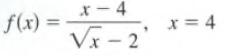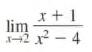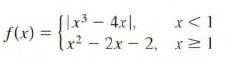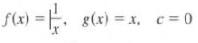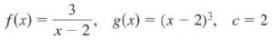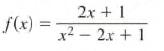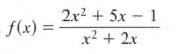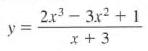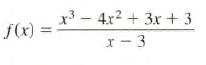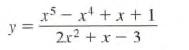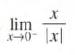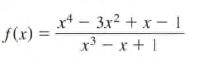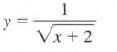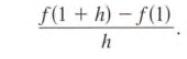Calculus Graphical, Numerical, Algebraic 3rd Edition Ross L. Finney, Franklin D. Demana, Bert K. Waits, Daniel Kennedy - Solutions

Unlock comprehensive insights with our exclusive resource for "Calculus Graphical, Numerical, Algebraic 3rd Edition" by Ross L. Finney and colleagues. Dive into online answers key and step-by-step solutions designed to enhance your understanding of complex calculus concepts. Our solution manual and solutions PDF provide detailed explanations for solved problems, making it an invaluable textbook companion. Access chapter solutions, questions and answers, and a test bank to prepare rigorously. Perfect for students and instructors alike, our free download option ensures you have the instructor manual and all necessary tools at your fingertips to excel in calculus.