There are n + 1 participants in a game. Each person independently is a winner with probability p. The winners share a total prize of 1 unit. (For instance, if 4 people win, then each of them receives 1/4, whereas if there are no winners, then none of the participants receives anything.) Let A denote a specified one of the players, and let denote the amount that is received by A.

a. Compute the expected total prize shared by the players.

b. Argue that

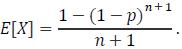
c. Compute E[X]  by conditioning on whether is a winner, and conclude that

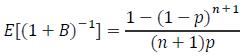
when is a binomial random variable with parameters and

Transcribed Image Text:

1- (1-р)"+1 E[X] 1-(1- п+1