(a) Show that F(z) = -(Ki/2Ï€) ln z with positive real K gives a flow circulating counterclockwise around z = 0 (Fig. 421). z = 0 is called a vortex.  Each time we travel around the vortex, the potential increases by K.

(b) Source and sink combined. Find the complex potentials of a flow with a source of strength 1 at z = -α and of a flow with a sink of strength 1 at z = α. Add both and sketch or graph the streamlines. Show that for small |α| these lines look similar to those in Prob. 19.

Data from Prob. 19

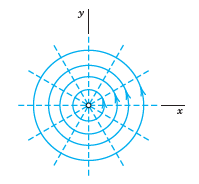
Show that the streamlines of F(z) = 1/z and circles through the origin with centers on the y- axis.

(c) Add the potential in (b) to that in Example 2. Show that this gives a flow for which the cylinder wall |z| = 1 is a streamline. Find the speed and show that the stagnation points are

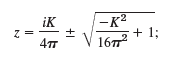
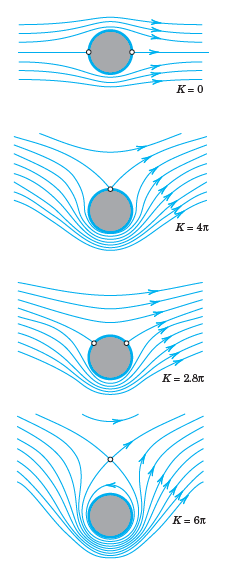
if K = 0 they are at ±1; as K increases they move up on the unit circle until they unite at z = i (K = 4Ï€, see Fig. 422), and if K > 4Ï€ they lie on the imaginary axis (one lies in the field of flow and the other one lies inside the cylinder and has no physical meaning).

Transcribed Image Text:

iK 4тт -к2 16т? + 1; +1