In Hermite interpolation we are looking for a polynomial p(x) (of degree 2n + 1 or less) such that p(x) and its derivative p'(x) have given values at n + 1 nodes. (More generally, p(x), p'(x), p"(x), · · · may be required to have given values at the nodes.)

(a) Let C be a curve in the xy-plane parametrically represented by r(t) = [x(t), y(t)], 0 ‰¤ t ‰¤ 1. Show that for given initial and terminal points of a curve and given initial and terminal tangents, say,

We can find a curve C, namely,

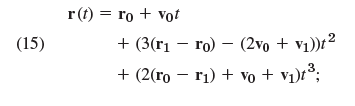
in components,

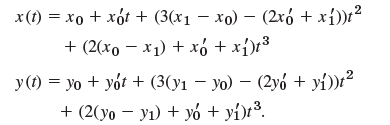
This is a cubic Hermite interpolation polynomial, and n = 1 because we have two nodes (the endpoints of C). (This has nothing to do with the Hermite polynomials in. The two points

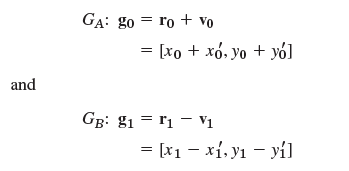
are called guidepoints because the segments AG_A and BG_B specify the tangents graphically. A, B, G_A, G_B determine C, and C can be changed quickly by moving the points. A curve consisting of such Hermite interpolation polynomials is called a Bezier curve, after the French engineer P. Bezier of the Renault Automobile Company, who introduced them in the early 1960s in designing car bodies. Bezier curves (and surfaces) are used in computer-aided design (CAD) and computer-aided manufacturing (CAM).

(b) Find and graph the Bezier curve and its guidepoints if A: [0, 0], B: [1, 0], v₀ = [1/2, 1/2], v₁ = [-1/2, -1/4ˆš3]

Transcribed Image Text:

А: Го — [x (0), у (0)] 3D [xо. Уol. B: r1 = [x(1), y(1)] = [x1, yı] Vo = [x'(0), y'(0)] — [x6. уб1. V1 = [r'(1), y'(1)] = [xí, yi] r(t) = ro + vot + (3(rı – ro) – (2vo + v1))t² + (2(ro – r1) + vo + v1)t³; (15)