The idea is that elementary operations can be accomplished by matrix multiplication. If A is an m x n matrix on which we want to do an elementary operation, then there is a matrix E such that EA is the new matrix after the operation. Such an E is called an elementary matrix. This idea can be helpful, for instance, in the design of algorithms. (Computationally, it is generally preferable to do row operations directly, rather than by multiplication by E.)

(a) Show that the following are elementary matrices, for interchanging Rows 2 and 3, for adding -5 times the first row to the third, and for multiplying the fourth row by 8.

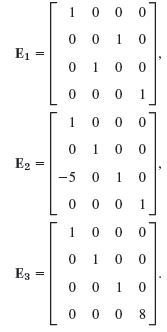
Apply E₁, E₂, E₃ to a vector and to a 4 x 3 matrix of your choice. Find B = E₃E₂E₁A, where A = [α_jk] is the general 4 x 2 matrix. Is B equal to C = E₁E₂E₃A? 

(b) Conclude that E₁, E₂, E₃ are obtained by doing the corresponding elementary operations on the 4 x 4. unit matrix. Prove that if M is obtained from A by an elementary row operation, then

M = EA,

where E is obtained from the n X n unit matrix I_n by the same row operation.

0 0 0 1 1 E1 = 1 1 0 0 1 E2 -5 0 1 1. 1 0 0