The last stage of a liquefaction process is shown in diagrammatic form in Fig. P18.2. Derive the relationship between \(p_{1}\) and \(T_{1}\) for the maximum yield of liquid at conditions \(p_{L}, T_{L}, h_{L}\) for a gas obeying the state equation

\[\left(p+\frac{1.368}{v_{m}^{2}}\right)\left(v_{m}-0.0367\right)=\Re T\]

where \(p\) is pressure (bar), \(v_{m}\) is the molar volume \(\left(\mathrm{m}^{3} / \mathrm{kmol}\right)\), and \(T\) is temperature \((\mathrm{K})\).

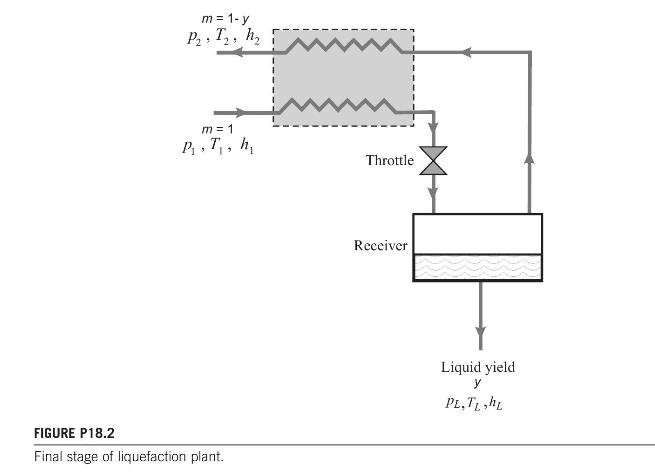
Calculate the pressure for maximum yield at a temperature of \(120 \mathrm{~K}\).
\[\left[p=\frac{a}{b^{2}}\left(1-\sqrt{\frac{\Re b T_{\mathrm{i}}}{2 a}}\right)\left(3 \sqrt{\frac{\Re b T_{\mathrm{i}}}{2 a}}-1\right) ; 62.8 \text { bar }\right]\]

Transcribed Image Text:

FIGURE P18.2 m = 1-y P, T, h 29 m=1 P, T, h 15 Throttle Final stage of liquefaction plant. Receiver Liquid yield y PL, TL,hL