Assume that (x) K x has distinct roots u 1 ,u 2 , , U n in the splitting field F and let G Aut K F n be the Galois group of Let Y 1 , , Y n be indeterminates and define (a) Show that (b) Show that g(x) K y 1 , , Y n ,x (c) Suppose g(x) factors as g 1 (x)g 2 (x) g r (x) with g i (x) K(y 1 , , Y n ) ...

ANSWER a We have gx x u1 Y1 u2 Y2 un Ynx u1 Y1 u2 Y2 un Yn x un Yn Expanding the product on the righthand side and using the fact that the roots of ar ...

Assume that (x) K[x] has distinct roots u 1 ,u 2 , ... , U n

Question:

Assume that ∫(x) ϵ K[x] has distinct roots u₁,u₂, ... , U_n in the splitting field F and let G = Aut_KF n be the Galois group of ∫. Let Y₁, . .. , Y_n be indeterminates and define: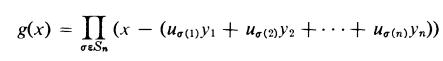

(a) Show that 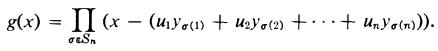(b) Show that g(x) ϵ K[y₁, ... , Y_n,x].

(c) Suppose g(x) factors as g₁(x)g₂(x)· · · g_r(x) with g_i(x) ϵ K(y₁, ... , Y_n)[x] monic irreducible. If is a factor of g₁(x), then show that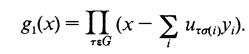

Show that this implies that deg g_i(x) = I GI.

(d) If K = Q, ∫ ϵ Z[x] is monic, and p is a prime, let ∫̅ ϵ Z_p[x] be the polynomial obtained from ∫ by reducing the coefficients of ∫(mod p). Assume ∫̅ has distinct roots u₁, ... , U_n in some splitting field F̅ over Z_P. Show that 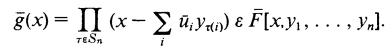If the u̅, are suitably ordered, then prove that the Galois group G̅ of ∫̅ is a subgroup of the Galois group G of ∫.