The cyclic group of order 4 has members (left{mathbf{E}, mathbf{A}, mathbf{B}=mathbf{A}^{2}, mathbf{C}=mathbf{A}^{3}ight}), and its product table is
Question:
The cyclic group of order 4 has members \(\left\{\mathbf{E}, \mathbf{A}, \mathbf{B}=\mathbf{A}^{2}, \mathbf{C}=\mathbf{A}^{3}ight\}\), and its product table is
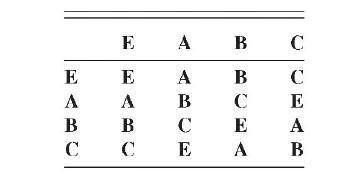
(a) What are the classes of this group?
(b) How many irreducible representations does this group have?
(c) What are the dimensions of its irreducible representations?
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction To Groups And Their Matrices For Science Students
ISBN: 9781108831086
1st Edition
Authors: Robert Kolenkow
Question Posted: