Consider the problem of how long it takes for a tank to drain. Consider an open-top cylindrical tank with one horizontal exit pipe at the bottom of the tank that discharges to the atmosphere. The tank has a diameter, d, and the height of liquid in the tank at any time is h.

The mass balance is unsteady state. Explain why the mass balance is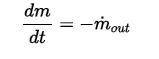

where m is the mass of liquid in the tank and

is the mass flowrate out of the tank.

The mass in the tank is the fluid density times the volume of liquid in the tank. The flowrate,

can be related to the velocity and the cross-sectional area of the exit pipe based on what we have already learned. The volume of liquid in the tank can be related to the height of liquid in the tank. Simplify the differential mass balance to obtain an expression for the height of liquid in the tank as a function of the velocity of the liquid through the exit pipe.

Now, write a mechanical energy balance on the fluid in the tank and pipe from the top level in the tank to the pipe outlet, neglecting friction. It is generally assumed the velocity of the tank level (i.e., the fluid level in the tank) is small because of the large diameter. Solve for the velocity, and rearrange the differential equation to look like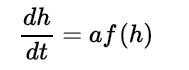

where a is a group of constants and f(h) is a function of the height that you have derived.

Solve this differential equation for height as a function of time with the initial condition of a height of h_o at time zero.

Rearrange the answer to Part (d) to get an expression for the time for complete drainage.

Transcribed Image Text:

dm dt II -mout