A lake is stocked with 100 fish. Let f (t) be the number of fish after t
Question:
A lake is stocked with 100 fish. Let f (t) be the number of fish after t months, and suppose that y = f (t) satisfies the differential equation y′ = .0004y(1000 - y). Figure 7 shows the graph of the solution to this differential equation. The graph is asymptotic to the line y = 1000, the maximum number of fish that the lake can support. How fast is the fish population growing when it reaches one-half of its maximum population?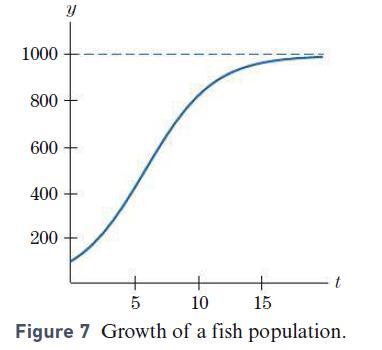
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus And Its Applications
ISBN: 9780134437774
14th Edition
Authors: Larry Goldstein, David Lay, David Schneider, Nakhle Asmar
Question Posted:





