Question: (a) Suppose A is obtained from A by applying an elementary row operation. Let C = AB, where B is any matrix of the appropriate

(a) Suppose A̅ is obtained from A by applying an elementary row operation. Let C = AB, where B is any matrix of the appropriate size. Explain why C̅ = A̅B can be obtained by applying the same elementary row operation to C.

(b) Illustrate by adding −2 times the first row to the third row of 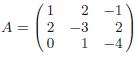A = 2-1 2 -4 1 2-3 0 1 and then multiplying the result on the right by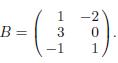

Check that the resulting matrix is the same as first multiplying AB and then applying the same row operation to the product matrix.

A = 2-1 2 -4 1 2-3 0 1

Step by Step Solution

★★★★★

3.29 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Suppose we have a matrix A and its transformed version A obtained by applying an elementary row op... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

Let A be an n n matrix. (a) Suppose that the matrix B is obtained from A by multiplying the jth row of A by k 0. Find an elementary row operation that, when applied to B, gives A. (b) Suppose that...

Exercise 5 implies that the effect of any elementary row operation can be reversed by another (suitable) elementary row operation. (a) Suppose that the matrix E1 is obtained from In by multiplying...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

1) Recall that the three types of elementary row operations are 1) multiplying a row by a scalar 2) interchanging two rows 3) Adding a multiple of one row to another Write three separate Python...

Elementary row operations 1) Recall that the three types of elementary row operations are 1) multiplying a row by a scalar 2) int rows 3) Adding a multiple of one row to another Write three separate...

l. [3 marks for each part) Solve each system of linear equations {over R]. Use Gauss-Jordan elimination {matrix row reduction). [at] {6] :r 23; 32 l 4:: 53; 62 l in: 83; +102 = l to +21 2y +3z = 2 2w...

For this assignment, you are to write a program to multiply two sparse matrices. You will implement a data structure that facilitates efficient processing of sparse matrices so that your program will...

Give the solutions please Solve the system by using elementary row operations on the equations. Follow the systematic elimination procedure. 7x1+14x2 = 14 5x1+7x2 = 3 Find the solution to the system...

1. Describe the possible echelon forms of a nonzero 2 x 2 matrix. (3 Select all that apply. (Note that leading entries marked with a I may have any nonzero value and starred entries ( * ) may have...

Q1: Q2: Fill up the blank in the below figure with the answers that explain the process of keying using Diffie-Hellman Key Agreement? Extract the public keys (PKs) and secret keys (SKs) . Consider...

A Francis turbine is required to give 180 kW output power under a net head (H) of 17 m. The efficiency is 80%. The turbine speed is 600 rpm. The flow velocity (V.) is constant and equals 0.3(2gH)2,...

Three single-phase, two-winding transformers, each rated 450 MVA. 20 kV/288.7 kV, with leakage reactance Xeq = 0.10 per unit, are connected to form a three-phase bank. The high-voltage windings are...

23. LO.13 What is a guaranteed payment? When is it deducted by the partnership? When is it reported in the recipient partners income?

11. How is the profitability index related to the NPV method? What does the PI measure?

Show that the matrix products A B and B A have the same size if and only if A and B are square matrices of the same size.

(a) Show that, if A and B are commuting square matrices, then (A + B)2 = A2 + 2AB + B2. (b) Find a pair of 2 2 matrices A and B such that (A + B)2 + A2 + 2AB + B2.

Show that if the matrices A and B commute, then they necessarily are both square and the same size.

Required information Skip to question [The following information applies to the questions displayed below.] During the year, TRC Corporation has the following inventory transactions. Date Transaction...

Handy Man, Inc., has zero coupon bonds outstanding that mature in 4 years. The bonds have a face value of $1,000 and a current market price of $798. What is the pretax cost of debt? (Use semiannual...

The most recent financial statements for Crosby, Incorporated, appear below. Interest expense will remain constant; the tax rate and the dividend payout rate also will remain constant. Costs, other...