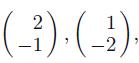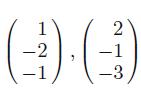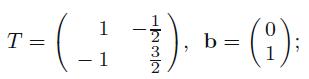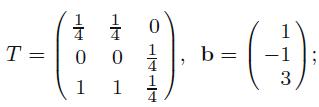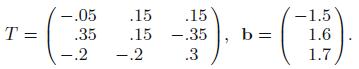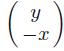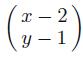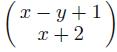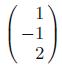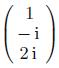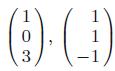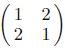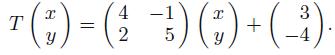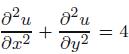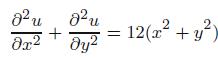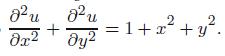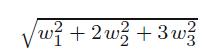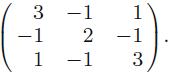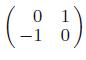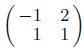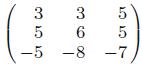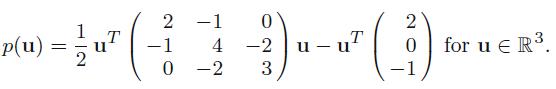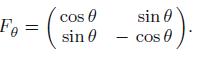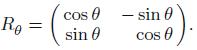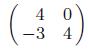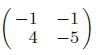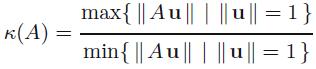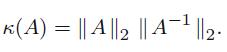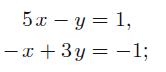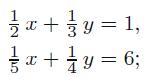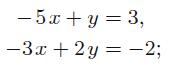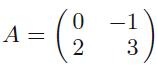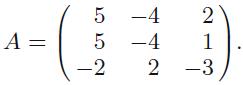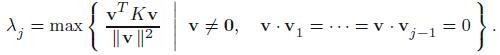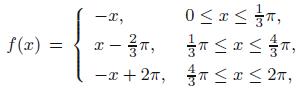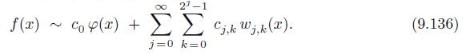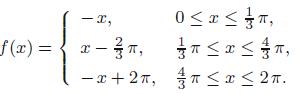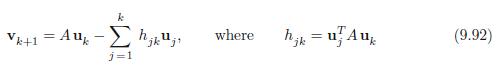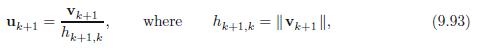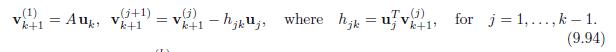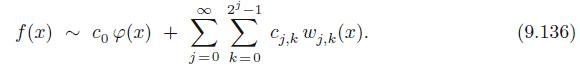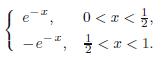Applied Linear Algebra 2nd Edition Peter J. Olver, Chehrzad Shakiban - Solutions

Discover comprehensive solutions for "Applied Linear Algebra 2nd Edition" by Peter J. Olver and Chehrzad Shakiban. Our platform offers an extensive range of online resources including answers keys, solution manuals, and chapter solutions. Explore step-by-step answers and a robust test bank to enhance your understanding of textbook content. With solved problems and instructor manuals available, we provide a thorough guide to mastering linear algebra concepts. Access the solutions PDF and other valuable materials for free download, ensuring you have the necessary tools to excel in your studies.