Answer Exercises 9.7.1 and 9.7.2 using the Daubechies wavelets instead of the Haar wavelets. Do you see any improvement in your approximations? Discuss the advantages and disadvantages of both in light of these examples.

Data From Exercise 9.7.1

Let f(x) = x. 

(a) Determine its Haar wavelet coefficients c_j,k. 

(b) Graph the partial sums s_r(x) of the Haar wavelet series (9.136) where j goes from 0 to r = 2, 5, and 10. Compare your graphs with that of f and discuss what you observe. Is the series converging to the function? Can you prove this? 

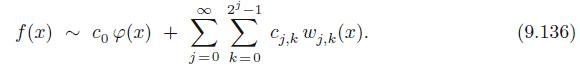
(c) What is the maximal deviation ΙΙ f − s_r ΙΙ_∞ = max{| f(x) − s_r(x) || 0 ≤ x ≤ 1} for each of your partial sums?

Data From Exercise 9.7.2

Answer Exercise 9.7.1 for the functions

(a) x² − x,

(b) cos πx,

(c)

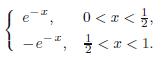
Data From Exercise 9.7.1

Let f(x) = x. 

(a) Determine its Haar wavelet coefficients c_j,k. 

(b) Graph the partial sums s_r(x) of the Haar wavelet series (9.136) where j goes from 0 to r = 2, 5, and 10. Compare your graphs with that of f and discuss what you observe. Is the series converging to the function? Can you prove this? 

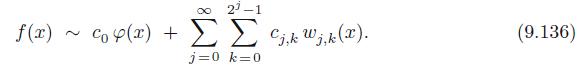
(c) What is the maximal deviation ΙΙ f − s_r ΙΙ_∞ = max{| f(x) − s_r(x) || 0 ≤ x ≤ 1} for each of your partial sums?

f(x) 2 cop(2) + 22-1 cjkW;;k(2). j=0 k=0 (9.136)