Let q_l(x) denote the trigonometric polynomial (5.119) obtained by summing the first 2l + 1 discrete Fourier modes. Suppose the criterion for compression of a signal f(x) is that For the particular function in Exercise 5.6.10, how large do you need to choose k when ε = .1? ε = .01? ε = .001?

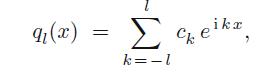
Data From Exercise 5.6.10

Construct the discrete Fourier coefficients for 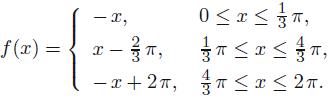based on n = 128 sample points. Then graph the reconstructed function when using the data compression algorithm that retains only the 11 and 21 lowest-frequency modes. Discuss what you observe.

|| f = 91 || = max{ |f(x) = q (x)||0 x 2 } < E