Develop an M-file to solve a single ODE with the midpoint method. Design the M-file so that it creates a plot of the results. Test your program by using it to solve for population as described in Prob. 22.5. Employ a step size of 5 years.

Data From Problem 22.5

Although the model in Prob. 22.4 works adequately  when population growth is unlimited, it breaks down when  factors such as food shortages, pollution, and lack of space  inhibit growth. In such cases, the growth rate is not a constant,  but can be formulated as

k_g = k_gm(1 − p/pmax)

where k_gm = the maximum growth rate under unlimited conditions, p = population, and p_max = the maximum population. Note that pmax is sometimes called the carrying capacity. Thus, at low population density p ≪ pmax, k_g → k_gm. As p approaches p_max, the growth rate approaches zero. Using this growth rate formulation, the rate of change of population can be modeled as

This is referred to as the logistic model. The analytical solution to this model is

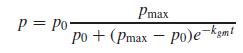
Simulate the world’s population from 1950 to 2050 using
(a) The analytical solution, and 

(b) The fourth-order RK method with a step size of 5 years. Employ the following initial conditions and parameter values for your simulation: p₀ (in 1950) = 2,560 million people, k_gm = 0.026/yr, and p_max =12,000 million people. Display your results as a plot along with the data from Prob. 22.4.

dp dt = kgm (1-P/Pmax) P