The drag coefficient for spheres such as sporting balls is known to vary as a function of the Reynolds number Re, a dimensionless number that gives a measure of the ratio of inertial forces to viscous forces:

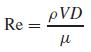
where ρ = the fluid’s density (kg/m³), V = its velocity (m/s), D = diameter (m), and μ = dynamic viscosity (N · s/m²).

Although the relationship of drag to the Reynolds number is sometimes available in equation form, it is frequently tabulated. For example, the following table provides values for a smooth spherical ball:

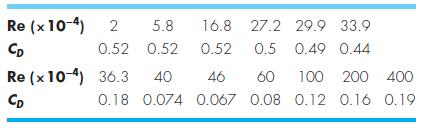
(a) Develop a MATLAB function that employs the spline function to return a value of C_D as a function of the Reynolds number. The first line of the function should be function CDout = Drag(ReCD,ReIn) where ReCD = a 2-row matrix containing the table, ReIn = the Reynolds number at which you want to estimate the drag, and CDout = the corresponding drag coefficient.

(b) Write a script that uses the function developed in part (a) to generate a labeled plot of the drag force versus velocity (recall Sec. 1.4). Use the following parameter values for the script: D = 22 cm, ρ = 1.3 kg/m³, and μ = 1.78 × 10⁻⁵ Pa · s. Employ a range of velocities from 4 to 40 m/s for your plot.

Re = pVD