For the buyers of two vehicle brands, you increase the strength of the motors in classified form. This results in the following contingency table:

(a) Indicate the expected frequencies in the case of statistical independence [in brackets under the actual number of observations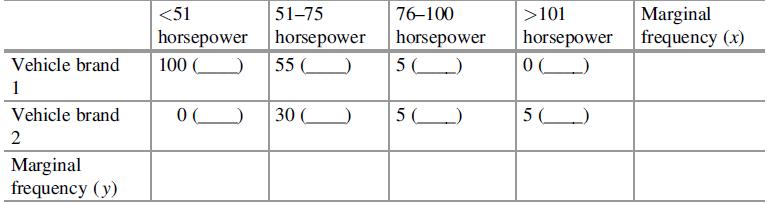

(b) What per cent of the purchasers of brand 1 bought a vehicle with between 76 and 100 horsepower?

(c) What per cent of purchased vehicles with a motor output of between 51 and 75 horsepower belong to vehicle brand 2?

(d) Briefly sketch how you would proceed with a chi-square test for statistical independence.

(e) Calculate the chi-square value so that the chi-square test is not distorted. On the basis of this chi-square value, can we conclude with a type 1 error of α = 1% that there is a statistical dependence between purchased vehicle brand and motor output?

(f) Say you increased the sample in the above example so that no rows or columns have to be aggregated. The chi-square value is now only 7.128. On the basis of this chi-square value, can we conclude with an error probability of α = 1% that there is a statistical dependence between purchased vehicle brand and motor performance?

Transcribed Image Text:

Vehicle brand 1 Vehicle brand 2 Marginal frequency (y) <51 horsepower 100 0( 51-75 horsepower 55() 30 ( 76-100 horsepower 5 5 C >101 horsepower 0(___) 5 (___) Marginal frequency (x)