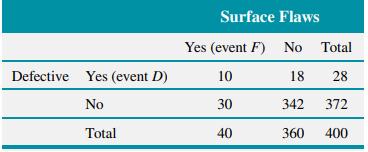
Again consider the 400 parts in Table 2.2. From this table,

\[ P(D \mid F)=\frac{P(D \cap F)}{P(F)}=\frac{10}{400} / \frac{40}{400}=\frac{10}{40} \]

Note that in this example all four of the following probabilities are different:

\[ \begin{array}{ll} P(F)=40 / 400 & P(F \mid D)=10 / 28 \\ P(D)=28 / 400 & P(D \mid F)=10 / 40 \end{array} \]

Table 2.2

Transcribed Image Text:

Defective Yes (event D) Surface Flaws Yes (event F) No Total No Total 10 18 28 30 342 372 40 360 400